Statistical physics
Statistical physics is a fundamental theory in physics that enables the study of macroscopic properties of physical systems in thermal equilibrium through their microscopic Hamiltonian. In recent years, the scope of statistical physics has been extended to encompass a diverse range of complex systems, spanning from physical and biological systems to technological and social systems. We apply statistical physics to understand the universal emergent collective phenomena, such as phase transitions and dynamic scaling behaviors, in various complex system.


1. Nonequilibrium phase transition
An interacting many-body system exhibits multiple macroscopic states, known as phases, and undergoes phase transitions between them as an external parameter changes. Phase transitions are a fascinating phenomenon of interacting many-body systems. We focus on nonequilibrium phase transitions in active matter systems composed of self-propelled particles. Self-propelled particles, including migrating birds, schooling fish, and swarming bacteria, demonstrate a phase transition between an ordered flocking phase and a disordered non-flocking phase. In the flocking phase, particles move collectively in a coordinated manner, while they move independently and randomly in the non-flocking phase. We investigate the mechanism and universality of the flocking transition using Monte Carlo simulations and analytic methods.
2. Quantum thermalization
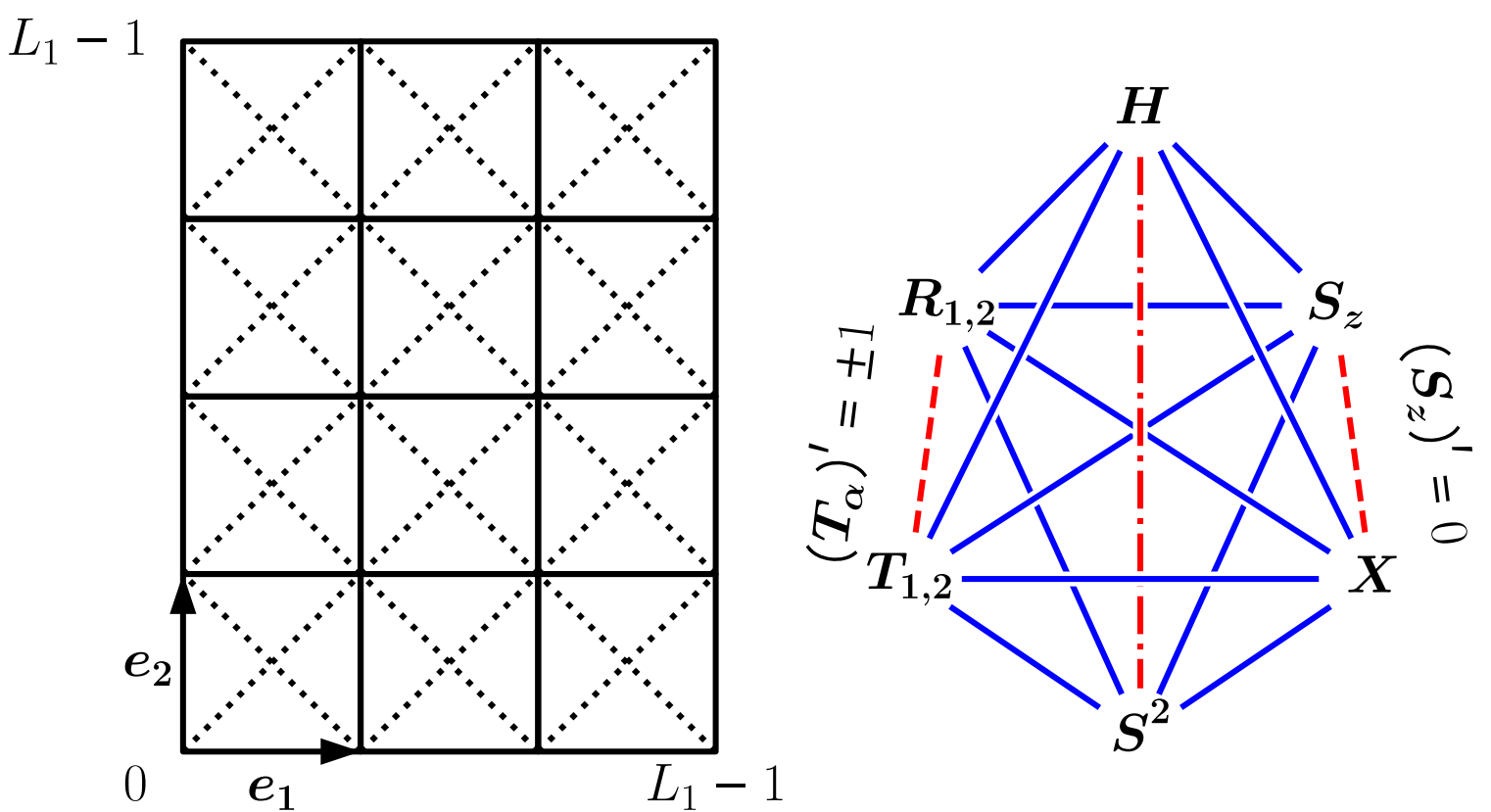
Statistical physics postulates that the thermal equilibrium property of an isolated system is described by the microcanonical ensemble. A crucial question arises: can an isolated quantum system attain thermal equilibrium through the unitary time evolution governed by the Schrödinger equation? The eigenstate thermalization hypothesis provides a promising explanation for the applicability of statistical physics to an isolated quantum system. We investigate the energy eigenvalue and eigenvector spectrum of various lattice spin systems to understand the mechanism of the quantum thermalization of isolated quantum systems.
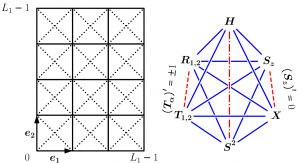

3. Complex System and Network Science
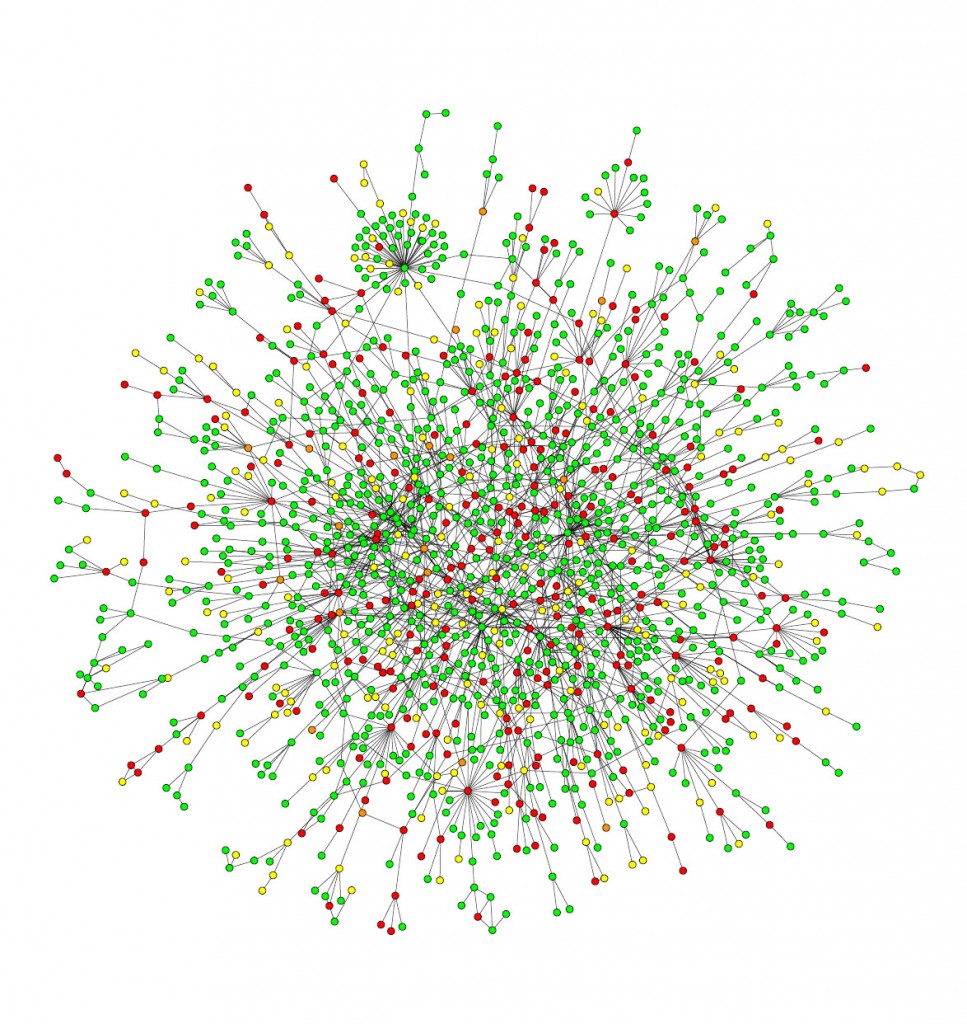
A complex system is a system composed of many interacting parts that exhibit emergent behavior that cannot be fully explained by understanding the behavior of its individual parts in isolation. This emergent behavior is the result of the collective phenomena that arise from the interactions between the components, rather than being the result of any single component acting alone. To study these complex systems, network science provides a way to represent them as networks of nodes and edges. By doing this, we can gain insight into how complex systems work, predict how they might behave in the future, and develop strategies for managing or optimizing them.
4. Human Mobility – Population
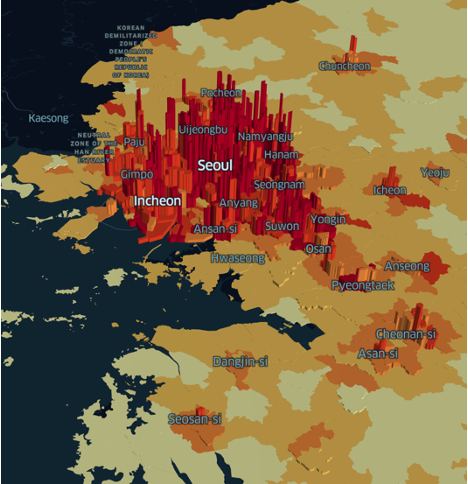
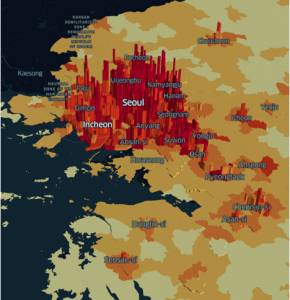
One example of using network science to study complex systems is in urban human mobility and population dynamics. By investigating the commuting pattern of populations as a network, we can determine the boundary between the urban and rural areas. In this case, areas become the nodes, and commuters become the edges. The results of this study show that each area can be classified into two types of habitat, urban and rural, by the ratio of self-commuting population in the area. This finding suggests that urbanization has a significant impact on the commuting pattern of the area.
5. Urban Transportation
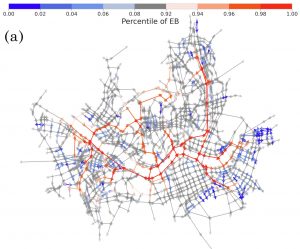
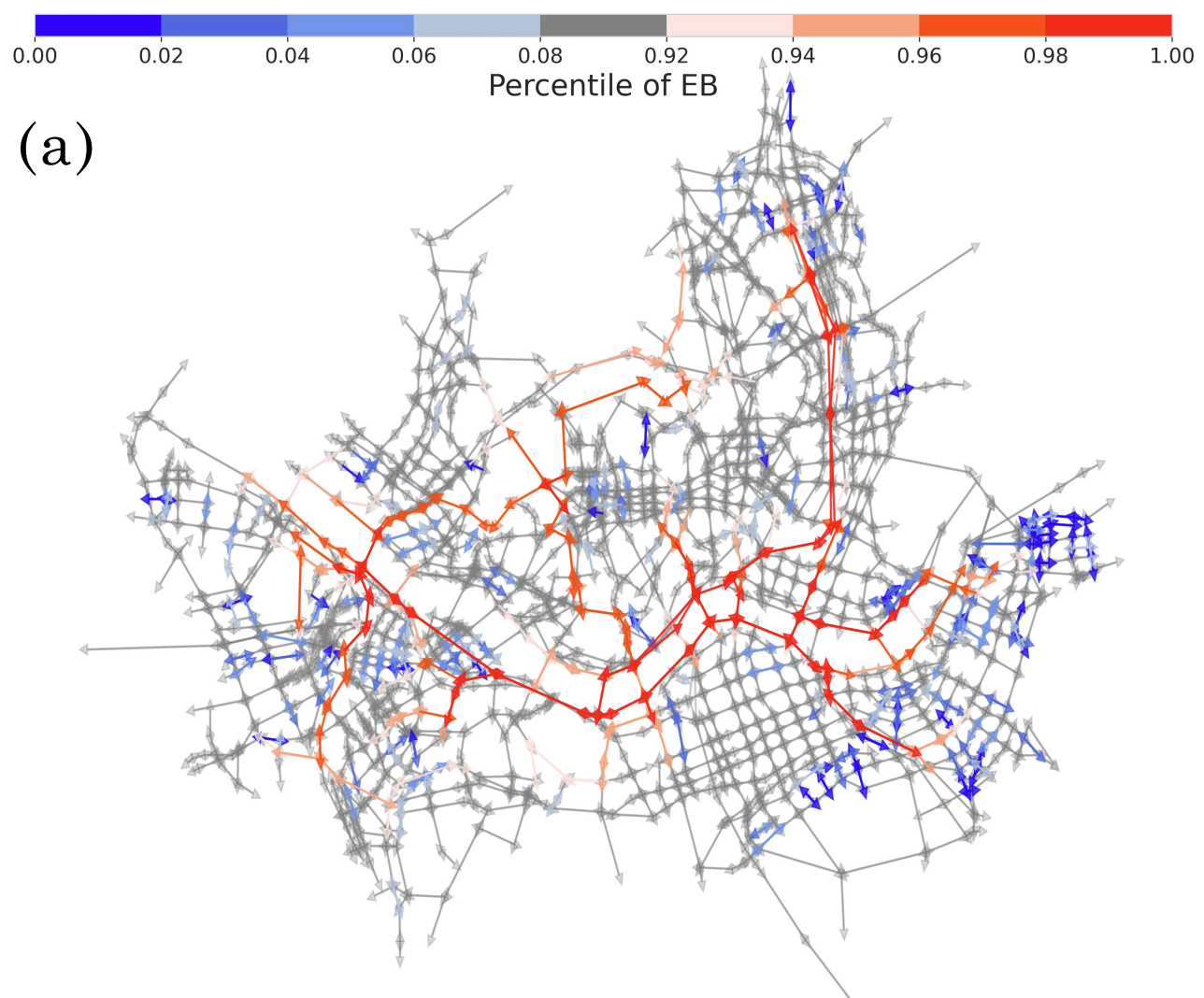
Another example is urban transportation, where both traffic flow and congestion can be studied as network phenomena. By applying the conventional percolation theory in statistical physics, we can identify the structural patterns of urban congestion and its evolution over time. This theory allows us to detect a shift in the backbone structure of the urban congestion network over time, which is the highway structure in terms of the connectivity, an important factor in the transportation system. We also found that the topological change affects the congestion duration of the urban traffic congestion. These examples illustrate how network science can provide a powerful tool for understanding the complex systems and collective phenomena that arise in urban environments.